Incremental and disruptive innovation are two of the raw distinctions how we categorize innovation. Incremental innovation comes in steps. Examples are the improvement of a production process, or the step-by-step reduction of exhaust emissions in a Diesel engine. Disruptive innovation seems to come in big jumps. Horse carriages that were pushed aside by cars, film that was replaced by digital cameras, and the cell phone that was swept away by smartphones.

But even disruptive innovation doesn’t come out of nowhere. Critics rightfully point out that a smartphone wasn’t really innovation. Touchscreens existed before, and also the computer chip used in smartphone was here for many years.

And they are right. Like in evolution man did not come out of the blue sky, but life had to manifest itself first in primitive forms to more complex organisms until we came to humans. Both evolution and innovation need the building blocks. If you combine building blocks we get new, more complex building blocks that allow to build even more complex objects. But you can only build them, when you have those building blocks available and created the opportunity to build with them. And then it becomes just a question of time until somebody makes this combination. Already in 1922 two researchers collected 140 examples, where innovators independently from each other made the same combination to create a new idea. Innovation becomes unavoidable.

This concept is called the ‘adjacent possible‘, which was introduced in 2002 by the complexity theoretician Stuart Kauffmann, So far this concept was rather difficult to describe, at least from a mathematical point of view. But now Vittorio Loreto at Sapienza and his colleagues from the Univerisyt of Rome came up with an addition to the model. At first, they start from the possibilities that innovation has. Starting from one point along paths you have multiple options for innovation.

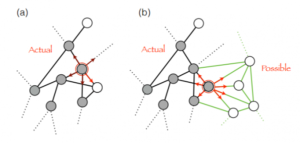The direction that innovation takes influences what future innovation is more likely to happen. The decision for a direction can have multiple reasons, but some future paths become more likely than others after innovation happened. Innovation influences future innovation and increase probabilities.

This model made it hard to put that into a mathematical model, if we want to understand the probabilities of innovation. And luckily, by using innovation and combining the adjacent possible with another model we can solve this. The Pólya Urn-model is what we need. The model was named after the Hungarian mathematician Pólya György and basically decribes this:

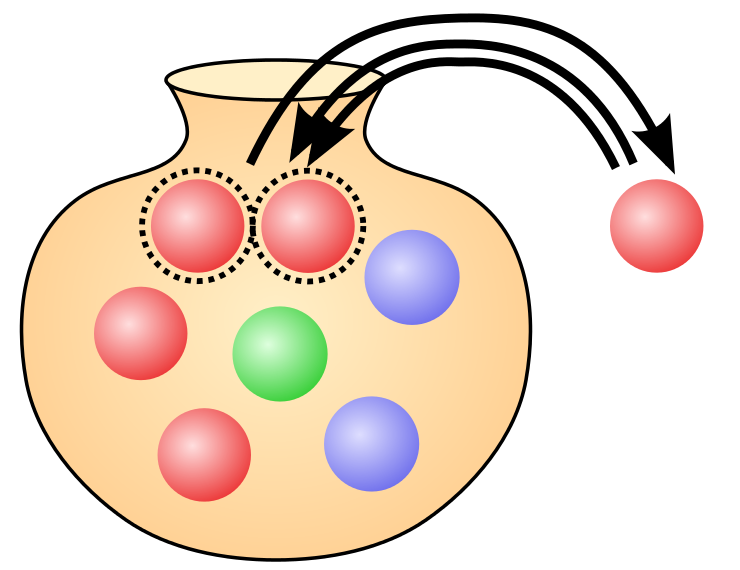
Imagine an urne (vase) filled with colored balls. Now we assume that of each of the red, blue, and green balls have the same number of balls in the urn. Once we pull one out and it’s a red one, we do not just toss one red ball back into the urn, but two of them. This way we change the distribution. We increase the probability that at the next drawing we get more likely a red one. By using this condition we will change the distribution of the balls towards some colors. Here is an example that demonstrates that very nicely.

Let’s assume that for each red ball drawn we don’t just add another red ball, but also a pink and a yellow one. This way we offer more possibilities and change the probabilities. The same happens with innovation. Each innovation adds possibilities.

With combining the models of the adjacent possible and the Pólya urn model we can describe innovation in a mathematical form. innovation becomes predictable. And innovation (something is new for humanity) as well as novelty (something is new for an individual) can be described.

For us that means something very interesting. Not only do we understand innovation better, and where it has to happen, but also a possible predictability of innovation. The vague and random seeming nature of innovation becomes palpable and potentially even projectable.

This article was also published in German.